题面翻译

在几何上，任何正方形都有一个唯一的中心点。在画有格子线的平面上，只有在正方形的边长为奇数时才成立。因为任何一个奇数都可以写成2k+1。所以若我们定义某一个正方形的大小为k，也就是表示他的边长为2k+1。现在我们要依照下面的规则来定义一个正方形所构成的图案：

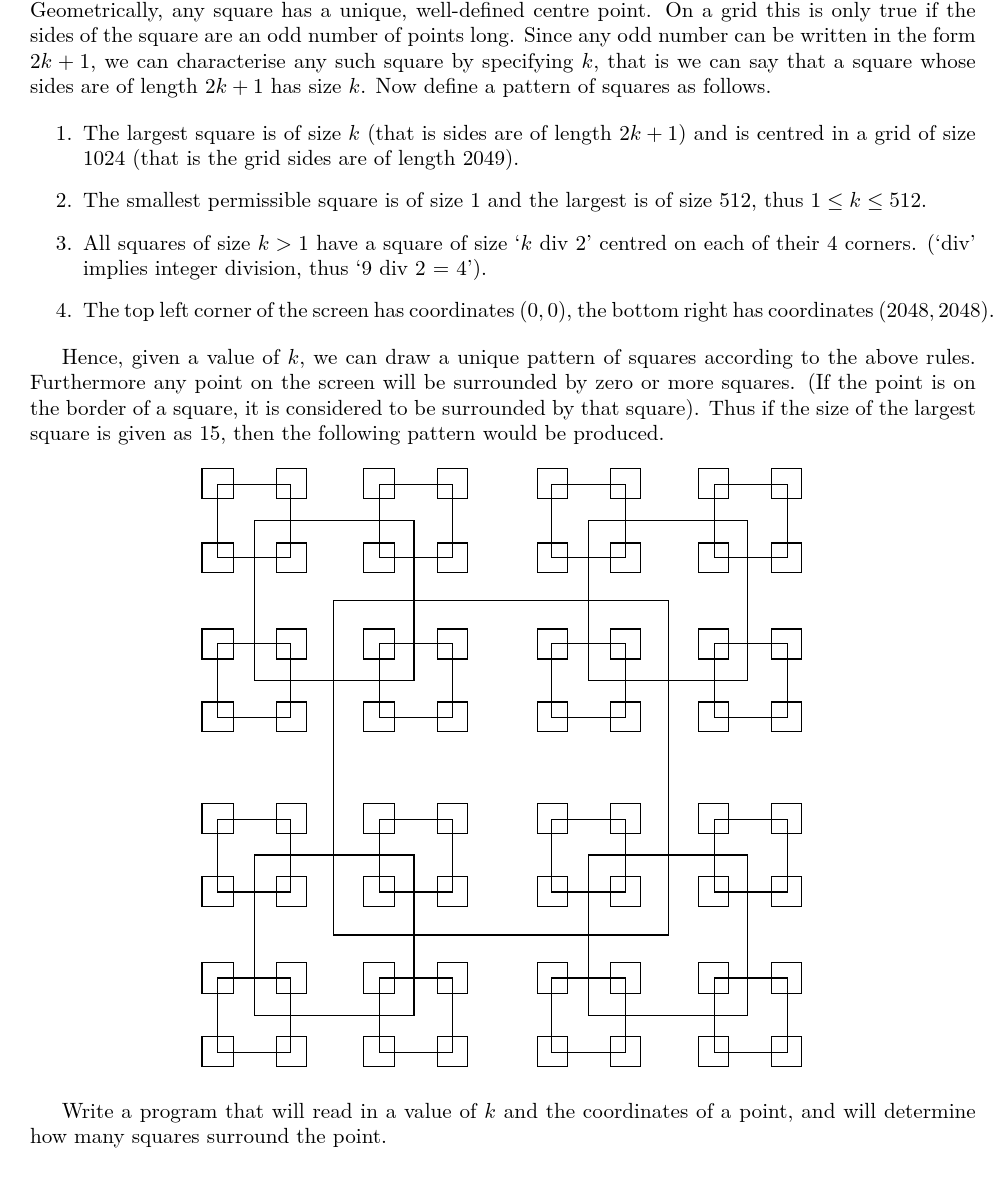
1.最大的正方形大小为k（也就是说边长2k+1）并且被放置在一个大小为1024的正方形的正中央。（也就是说整个可以使用的区域为一个边长2049的正方形，如以座标表示，此区域左上角座标为（0,0），右下角座标为（2048,2048）） 2.可以允许使用的正方形大小最小为1,最大为512。因此 1<= k <= 521。 3.所有 k>1 的正方形，以其4个角为中心点各有一个大小为 k div 2 的正方形（在这裡div指的是整数的除法，例如：9 div 2 = 4） 因此，给你一个k值，根据以上的规则，我们可以画出一个唯一的图案。而萤幕上的每一个点可能落在0个或多个正方形中。（我们定义若点刚好落在边上，亦视为落在此正方形中）。所以如果最大的正方形的k=15，我们可以画出以下的图案：

（如图）

写一个程式，读入k及某一个点的座标，输出该点总共被多少个正方形所包围。

Input

每组测试资料一列，每列有3个整数。分别代表k及一个点的座标。最后一列的内容为3个0，代表输入结束。

Output

每组测试资料输出一列。输出该点总共被多少个正方形所包围，输出长度为3，靠右对齐。

感谢@ibuki320 提供的翻译

题目描述

PDF

输入格式

输出格式

样例 #1

样例输入 #1

500 113 941
0 0 0

样例输出 #1

5